FIZIKA
Dalibor Čevizović
Kvantna prepletenost
”Dejstvo duhova na daljinu”
Kvantna prepletenost je, verovatno, jedna od najčudnijih i verovatno zbog toga jedna od najmistifikovanijih osobina kvantnih sistema. Za nju znamo maltene od prvih koraka u kvantnoj fizici, čak je stekla i veliku popularnost u naučnoj fantastici. Ipak, u praksi dugo nije imala neku značajniju ulogu. Lako se, međutim, može desiti da ona u bliskoj budućnosti odigra ključnu ulogu na polju primenjene kvantne mehanike, na primer u teoriji procesa kvantnih merenja, kvantnoj informatici, pogotovo u zaštiti podataka, čuvanju, procesu prenosa i obrade kvantne informacije. Kvantna teleportacija, kvantni kompjuteri, kvantna kriptografija, kvantni novac i kvantno bankarstvo samo su neki od pojmova koji se u naučnoj literaturi sve češće sreću, a koji u osnovi imaju kvantnu prepletenost. Osim toga, postoje ozbiljne naznake da ova pojava igra važnu ulogu u živom svetu. Čini se, naime, da mogućnost orjentacije u magnetnom polju nekih ptica selica tokom njihovih migracija može da se objasni procesima u kojima prepletena kvantna stanja para elektrona imaju ključnu ulogu.

Kako danas stvari stoje, ptice registruju (možda je bolje reći: mere, jer registrovati znači samo osetiti prisustvo, a izmeriti znači osetiti prisustvo, ali i odrediti pravac i smer!) magnetno polje pomoću koherentnosti spinskih stanja para elektrona u proteinima! Pri tome, ova koherentnost uspeva da se u proteinima i dovoljno dugo održi. Osim toga, izgleda da kvantna prepletenost ima izvesnu ulogu u formiranju i održavanju oblika dvostruke spirale kod DNK. Ali, o tome na nekom drugom mestu. Ovde ćemo pokušati da čitaocu približimo ovu čudnu i našim svakodnevnim predstavama stranu osobinu.
Mala ekskurzija u osvit kvantnomehaničke povesti
Zakoni klasične fizike su u potpunosti deterministički. Za statistikom ona poseže (i to iz čisto praktičnih, a ne principijelnih razloga) tek onda kada je poznavanje stanja posmatranog sistema nepotpuno. Na primer, kod sistema koji se sastoje od velikog mnoštva čestica, poznavanje stanja u kojem se nalazi svaka pojedina čestica praktično je nemoguće. Ipak, ponašanje i osobine ovakvih sistema pokazuju izvesnu pravilnost koju je moguće opisati uz pomoć zakona statistike.
Za razliku od klasičnog, kvantni sistem je po samoj svojoj suštini statistički. Njegov statistički karakter nije povezan sa nepotpunošću poznavanja stanja u kojem se kvantni objekat nalazi, već je posledica osobenosti mikrosveta. Čime opisati stanje kvantnog objekta? Kad kažemo da se kvantni objekt nalazi u nekom (određenom) stanju, podrazumevamo da postoji spisak (katalog, kako je to lepo govorio Ervin Šredinger) ili što je isto, funkcija koja sadrži informaciju o svim mogućim rezultatima merenja neke opservable (opservablom se u kvantnoj mehanici podrazumeva neka opservabilna veličina) ili određenog skupa opservabli nad tim objektom.
Ako izvršimo seriju jednakih merenja nad istim kvantnim objektom, dobijeni rezultati najčešće će se razlikovati od merenja do merenja. Ovde pod terminom isti kvantni objekt podrazumevamo da je posle izvršenog merenja kvantni objekt na neki način ponovo doveden (pripremljen) u prvobitno stanje. Međutim, postoji i drugi način da se ovo postigne: uzmemo dovoljno velik broj istovrsnih kvantnih objekata pripremljenih u isto stanje, a zatim nad svakim pojedinačno izmerimo istu fizičku veličinu!
Zato entitet kojim želimo da opišemo stanje kvantnog sistema mora dati statističku informaciju (funkciju raspodele) za svaki mogući rezultat merenja date fizičke veličine. Ovakva funkcija kojom u kvantnom svijetu opisujemo stanje kvantnog objekta zovemo funkcijom stanja kvantnog sistema. Kakve osobine ima skup svih fukcija stanja posmatranog kvantnog objekta?
Novembra 1935. godine Ervin Šredinger je u časopisu „Die Naturwissenschaften“ objavio rad pod nazivom „Savremeno stanje kvantne mehanike“. Po rečima samog Šredingera, rad je plod diskusije koja se rasplamsala nakon objavljivanja čuvenog rada Alberta Ajnštajna, Borisa Podolskog i Natana Rozena, „Da li je kvantni opis realnosti potpun?“, objavljenog u časopisu „Physical Review“. U svom radu Šredinger analizira neka osetljiva mesta u teoriji merenja nad kvantnim sistemima. Pri tome formuliše četiri postavke prema kojima stanja kvantnih objekata poseduju sledeća svojstva:
1. superpozicija (kvantna stanja mogu da se prikažu u obliku linearne superpozicije nekih osnovnih, bazisnih stanja);
2. interferencija (rezultat merenja zavisi od relativne faze amplituda superponiranih stanja);
3. prepletenost (čak i kad potpuno poznajemo stanje u kojem se nalazi kvantni sistem, to ne znači da potpuno poznajemo stanje u kojima se nalaze njegovi delovi. Pri tome, potpunost poznavanja stanja ovde se uzima u kvantno-mehaničkom smislu);
4. neodređenost i nemogućnost kloniranja (kvantni sistem ne možemo posmatrati a da na njega ne utičemo. Takođe, nepoznato stanje kvantnog sistema ne možemo klonirati. Može neko da se zapita: zašto se ovde ističe da je stanje kvantnog objekta kojeg želimo da kloniramo nepoznato? Razlog je sledeći: ako je stanje kvantnog objekta poznato (npr. stanje atoma vodonika), prosto možemo uzeti drugi identičan kvantni objekt (atom vodonika) i dovesti ga u stanje prvog objekta).
Superpozicija kvantnih stanja
Kao što smo rekli, funkcija stanja kvantnog sistema mora da poseduje izvesne osobine, među koje spada i osobina da se iz nekog skupa osnovnih, bazisnih stanja, mogu dobiti druga, složena stanja koja takođe odgovaraju mogućim rezultatima merenja posmatrane fizičke veličine na posmatranom kvantnom objektu. Pogledajmo ovo na primeru sistema koji može da se nađe u samo dva kvantna stanja, na primer fotona u stanju linearne polarizacije.
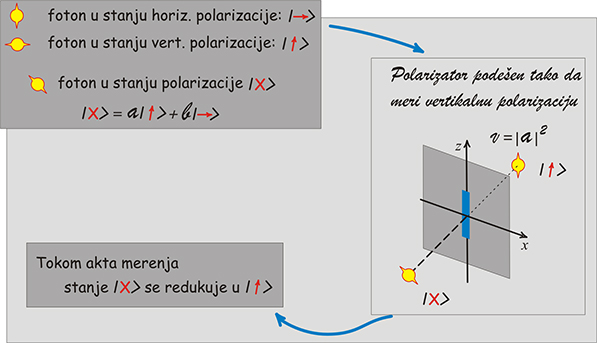
Ako za bazisna stanja odaberemo stanje horizontalne polarizacije i stanje vertikalne polarizacije, tada je i |x) takođe stanje u koje foton može da se pripremi. Pri tome kompleksni brojevi a i b određuju učešće stanja vertikalne, odnosno stanja horizontalne polarizacije u stanju |x). Kažemo da je |x) koherentna smesa (superpozicija) bazisnih stanja. Pođimo i korak dalje: ako foton pripremljen u stanje |x) usmerimo ka analizatoru podešenom da propušta fotone sa vertikalnom polarizacijom, on će kroz analizator proći sa verovatnoćom v. |
Tokom procesa merenja (međudelovanje kvantnog objekta sa makroskopskim mernim priborom), prvobitno stanje kvantnog objekta se nepovratno ruši (trpi redukciju), a sam kvantni objekat se, nakon izlaska iz mernog pribora, nalazi u nekom drugom stanju (koje zavisi i od podešavanja mernog pribora)!
Moguće je, međutim, merni pribor podesiti na takav način da kvantni objekat sa sigurnošću prolazi kroz njega. Tada kvantni objekat ne menja svoje stanje. Na primer, ako foton u stanju vertikalne polarizacije napravimo na analizator pripremljen tako da propušta fotone baš u tom stanju, on će sa sigurnošću proći kroz analizator, a stanje fotona, nakon izlaska iz uređaja, biće identično onom pre nailaska na analizator. Drugim rečima, rezultat merenja nad kvantnim objektom koji je pripremljen u neko određeno stanje zavisi od toga šta meri naš merni pribor.
Sve ovo neodoljivo podseća na osobine talasa koji se prostiru u nekoj materijalnoj sredini (npr. talase u vodi, vazduhu...). Zato se matematički entiteti kojima opisujemo stanja kvantnih objekata ponekad zovu talasne funkcije. Problem je u tome što se talasi u materijalnoj sredini prostiru kroz konkretan medij. Talasne funkcije (iako imaju iste matematičke osobine kao i funkcije kojima opisujemo materijalne talase) ne prostiru se kroz neku sredinu: oni su prosto matematički objekti koji nam služe da izračunavamo verovatnoće rezultata merenja nad kvantnim objektima. Matematički gledano, skup svih funkcija stanja kvantnog objekta obrazuje vektorski prostor (nad kompleksnim poljem).
Recimo još samo, zašto se traži da stanje |x) bude koherentna smesa bazisnih stanja? Kad bi superpozicija bila nekoherentna, kad bi svaki od bazisnih vektora imao nezavisnu fazu pri čemu im se fazna razlika sa vremenom menja (nekoherentnost), stanje |x) ne bi bilo stabilno! Praktično to znači da bi se u jednom momentu kvantni objekat u pomenutom stanju nalazio a već u sledećem on bi iz njega iščezao! I to bez uticaja bilo kakvog spoljnog dejstva.
Paradoks Šredingerove mačke
Da bi istakao neobičan karakter stanja nastalih superpozicijom, Šredinger je zamislio „eksperiment“ čiji se rezultat u potpunosti kosi sa našim svakodnevnim poimanjem prirode. Pretpostavimo da je Šredinger u sanduk stavio svojeg kućnog ljubimca, mačku. Kutija nije bilo kakva, ona je snabdevena posudicom sa otrovom i izvorom jonizujućeg zračenja (male aktivnosti). Posudicu može da razbije mehanizam koji je spojen sa detektorom jonizujućeg zračenja: kad detektuje raspad jedne čestice, detektor odašilje impuls koji pokrene mehanizam. Radioaktivni atom (budući da je on kvantni objekt) se nalazi u superponiranom stanju: stanja u kojem se s određenom verovatnoćom raspao, i stanja u kojem je sa određenom verovatnoćom neraspadnut. Tada se, međutim, tačno u takvom superponiranom stanju nalazi i Šredingerova mačka: s određenom verovatnoćom ona je mrtva, a sa određenom - živa!
 |
U slučaju mikroskopskih sistema, takvih kao što su atomi ili molekuli, superpozicija stanja je obična stvar, koju lako detektujemo. Međutim, u slučaju makroskopskih sistema kakva je mačka, ovakva superpozicija se ne opaža. Očigledno, postoji neki razlog koji u makrosvetu dovodi do rušenja superpozicije (dekoherencije). U poslednje vreme pojavila su se mišljenja da baš ovde treba tražiti kopču koja povezuje kvantni svet sa gravitacijom: kopča koja bi omogućila ostvarenje davnašnjeg sna Alberta Ajnštajna i generacija teorijskih fizičara o postuliranju jedinstvene slike materijalnog sveta. Pomenimo još samo da je problem očuvanja superponiranih stanja kod mezosistema aktuelan zadatak, posebno u teoriji kvantne informacije.
Prepletena stanja
Uporedo sa stanjima nastalim (koherentnom) superpozicijom, Šredinger razmatra i tzv. prepletena stanja (u anglojezičnoj literaturi ova stanja se zovu entangled states, dok se u ruskojezičnoj literaturi zovu перепутанные ili запутанныесостояния). Ovakva stanja su mu bila potrebna da bi opisao stanja nekog složenog sistema koji se sastoji od dvaju ili više podsistema (u najprostijem slučaju, dva kvantna objekta) koji su jednom nastali u istom fizičkom procesu, i usled čega su ovi na neki način povezani, ili kako neki vole da kažu korelisani. Možemo, na primer, imati posla sa dva elektrona suprotnih spinova, ili dva fotona koji poseduju određena stanja polarizacije. Ali, pođimo od početka.
Gledajući unazad, celoj priči podsticaj je dao pomenuti Ajnštajnov rad iz 1935. godine. Nećemo se baviti Ajnštajnovim razlozima zašto je uopšte pisao ovaj rad. Ono što je iz diskusije koju je izazvao ovaj rad izraslo, sasvim je druga, za nas interesantna priča. Pomenuti rad je pokrenuo žučnu diskusiju u čijoj osnovi leži tzv. EPR paradoks. Da bi oborio tada već prihvaćenu tzv. Kopenhagensku interpretaciju kvantne mehanike, Ajnštajn razmatra sistem dva elektrona, u kojem se održava ukupan impuls (u ovom primeru, zakon održanja impulsa predstavlja pomenutu korelaciju). U radu Ajnštajn ukazuje da bi intervencija na jednom od elektrona trenutno uticala na drugi iz pomenutog para, što je, prema onom što nam govore zakoni fizike, nemoguće jer se ništa ne može prostirati trenutno! Međutim, umesto da postigne željeni cilj, svetlost dana ugledao je nov problem! Još uvek je maglovito? Naravno! Da bi malo razmaglili situaciju, pogledaćemo neke primere.

Sa čisto formalnog, matematičkog gledišta, stanja u kojima se dvočestični kvantni sistem može naći mogu biti separabilna (kada se vektor stanja celog sistema može prikazati u obliku direktnog proizvoda vektora stanja prve, odnosno drug čestice) i neseparabilna. Ova druga situacija odgovara slučaju kad se par nalazi u prepletenom stanju. |
Dve paradoksalne osobine dvočestičnog sistema u prepletenom stanju
Još jednom, ističemo važnost korelacije koja mora da postoji između delova sistema koji se nalazi u prepletenom stanju. Objasnimo ovo na primeru fotonskih parova koji se nalaze u tzv. Belovim stanjima. Ova stanja je Džon Bel uveo upravo zato da bi razmotrio EPR paradoks. U slučaju kada se oba fotona nalaze u stanju linearne polarizacije, bazisna Belova stanja mogu da se odaberu u sledećem obliku:
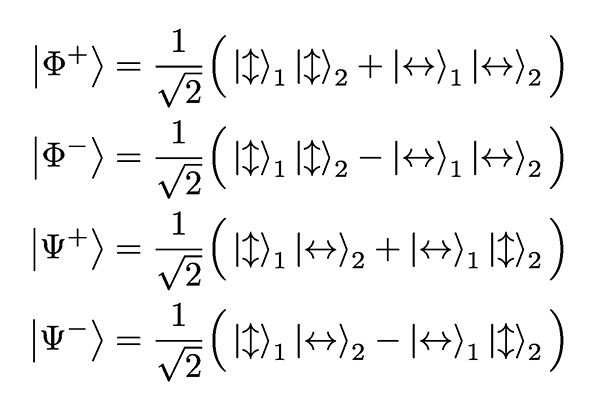
ovde indeksi ukazuju kojem od jednofotonskih podprostora pripada vektor. U prva dva stanja korelaciju predstavlja podatak da se par fotona nalazi u istom stanju polarizacije, dok je korelacija u druga dva stanja podatak (osobina) da se par fotona nalazi u suprotnom stanju polarizacije. Osim toga, 1. i 2., kao i 3. i 4. stanje se razlikuju po svojim simetrijskim osobinama. |
Zamislimo da smo par fotona pripremili u neko od Belovih prepletenih stanja. Nakon izvesnog vremena, izvršimo merenje na samo jednom od fotona iz para. Svako od ovih prepletenih stanja ima interesantnu i začuđujuću osobinu: čim se u procesu merenja jedan od fotona projektuje u stanje sa određenom polarizacijom, istog momenta polarizacija drugog fotona takođe postaje tačno određena! Na primer, ako je dvofotnoski sistem bio u trećem od Belovih stanja, i ako na jednom od fotona detektujemo stanje vertikalne polarizacije, istog momenta stanje polarizacije drugog fotona postaje suprotno: on postaje horizontalno polarisan. I sad se javlja ono važno pitanje: kako merenje izvršeno nad jednom česticom može trenutno da utiče na stanje u kojem se nalazi ona druga? I to bez obzira na njihovo rastojanje, jer druga čestica može biti proizvoljno daleko! Na izvestan način ovo ruši celu teškom mukom sagrađenu sliku o interakciji dvaju fizičkih objekata koja je bila uobličena tek nekoliko decenija pre pojave kvantne mehanike.
Sliku koja se zasnivala na konceptu fizičkog polja i koja je jednom za svagda predstavu o neposrednom (i trenutnom) dejstvu jednog tela na drugo (a kakvu su u vidu imali Njutn i Kulon) izbacila iz fizike izgleda da se Ajnštajnu (i ne samo njemu!) ovo učinilo kao korak u nazad. Kao vraćanje nekim starim predodžbama. Možda bi tako i bilo da je povezanost kvantnih podsistema zasnovana na konceptu interakcije (koja bi opet zahtevala određeno fizičko polje). Ali, ovde su u pitanju korelacije! I to je bitna razlika! Kod kvantne prepletenosti, interakcije (pa time i fizičkog polja) nema. Ali postoji korelacija između objekata koji grade sistem. Bez obzira na to, Ajnštajn ovako nešto nikad nije svario pa je ceo koncept ironično nazvao "`dejstvo duhova na daljinu"'. Do danas je međutim, pomenuto svojstvo prepletenih stanja demonstrirano u nizu eksperimenata.
U čemu je ovde protivrečnost? Pogledajmo primer koji se često navodi pri objašnjenju kvantnog preplitanja u naučno-popularnim prikazima.
Par rukavica
Zamislimo da imamo dve rukavice (levu (L) i desnu (D)), pa ih stavimo u dve neprozirne i po svemu jednake kutije. Slučajnim izborom, u istom momentu ekspres poštom jednu kutiju pošaljemo Ani u Dubnu, a drugu Branku u Vinču. Za vreme putovanja, kutije sa rukavicama su u prepletenom stanju: kutije su dva jednaka objekta (koji čine sistem), međusobno povezana korelacijom "u obe kutije ne može biti rukavica iste vrste". Dakle, ulogu kvantnih objekata ovde igraju kutije, ulogu kvantnih stanja igra osobina leva rukavica, odnosno desna rukavica (opet imamo dvočestični sistem gde se svaka od čestica može naći u dva stanja) a ulogu korelacije činjenica da u paru rukavica obavezno imamo jednu levu i jednu desnu.
Neka su obe kutije na odredište stigle u istom trenutku. Ni "A" ni "B" ne znaju kakvu su rukavicu poštom dobili: kutije su još uvek u prepletenom stanju. I za jedno i za drugo postoji 50% verovatnoće da je kod njega kutija sa L, odnosno 50% verovatnoće da je kod njega kutija sa D rukavicom.
Onog trenutka međutim, kad neko od njih (npr. "B") otvori kutiju (izvrši ogled) i ugleda rukavicu (dobije rezultat merenja) (npr. L), u istom tom momentu kod drugog ("A") je verovatnoća pojavljivanja rukavice L postala jednaka 0 (kolapsirala je) a verovatnoća pojavljivanja rukavice D postala 1! "A" uopšte i ne mora da otvara svoju kutiju: “B" može da joj informaciju saopšti pomoću goluba-pismonoše (recimo, da je maksimalna brzina prostiranja informacije u njihovoj vasioni jednaka brzini leta goluba).
Pa, šta je tu paradoksalno?
1) Paradoksalno je to što je verovatnoća pojavljivanja rukavice L kod "A" pala na 0 u istom trenutku u kojem je "B"' video da je dobio rukavicu L! Pre nego što je golub mogao da doleti od "B” do "A" (odnosno, pre nego je do "A" mogla da dođe bilo kakva informacija).
2) (ovo zvuči još paradoksalnije) I sve do momenta merenja koje je sproveo "B", kod "A" su postojale obe mogućnosti (odnosno, on je sa istom verovatnoćom mogao da dobije i drugačiji rezultat).
Ili da ovo obojimo još jarkije: neka su "A" i "B" unapred uskladili svoje časovnike i dogovorili se da će određenog dana (kad oboje prime pošiljke: u njihovoj vasioni pošta je pouzdana institucija i sa sigurnošću je moguće predvideti prijem neke pošiljke, u zavisnosti od rastojanja s kojeg ona stiže), tačno u podne, "B" zaviriti u svoju kutiju. Po istom tom dogovoru, "A" će svoju kutiju otovoriti trenutak kasnije. Ovaj trenutak je dovoljno kratak da nikakva informacija od "B" ka "A" nije mogla da stigne (pa ni golub pismonoša). Kao što smo rekli, ako je "B" kod sebe našao rukavicu L, "A" ć kod sebe obavezno ugledati rukavicu D. Ali, da je samo tren ranije u odnosu na "B" otvorila svoju kutiju, mogla je sa istom verovatnoćom da ugleda ili L ili D rukavicu! I pri tome, sve vreme govorimo o jednoj te istoj pošiljci! Da je ona tada ugledala L rukavicu, "B" bi po otvaranju svoje kutije nužno konstatovao da je kod njega rukavica D! A ovo se već uveliko kosi sa "zdravim razumom", ili bolje rečeno s onim na šta nas privikava životna svakodnevica.
Po mom mišljenju, problem nastaje u sledećoj situaciji: šta ako su se "A" i "B" dogovorili da svak u svoju kutiju zavire u istom trenutku? Ova situacija pomalo liči na probleme sa singularnostima i ja kao autor ovog teksta, nemam odgovor na njega.
Bertlmanove čarape
Kakve veze sa svim ovim imaju Bertlmanove čarape? I ko je uopšte taj Bertlman?
Elem, prof. Bertlman je jedno vreme u CERN-u radio zajedno sa Džonom Belom. Bel je napisao rad "Bertlmanove čarape i priroda realnosti" u kojem je iskoristio Bertlmanovu rasejanost kao šaljivu alegoriju, uprošćeni primer determinističkog shvatanja EPR paradoksa. I kako to već biva u istoriju fizike, kvantne prepletenosti su zajedno ušli: Bel sa svojim stanjima i (ne)jednačinama, ali i Bertlman sa svojim čarapama.
Reinthold Bertlman je profesor na Bečkom univerzitetu, koji je osim po svojim istraživanjima, poznat i po velikoj, u akademskim krugovima čestoj, rasejanosti. Gotovo po pravilu je na predavanja dolazio u nesparenim čarapama. Nemoguće je bilo unapred pogoditi na kojoj nozi mu je čarapa koje boje. Međutim, dovoljno je bilo da ako mu, na primer, na levoj nozi ugledate ljubičastu čarapu, odmah znate da mu je na desnoj čarapa bilo koje boje, samo ne ljubičaste. |
Dalibor Čevizović
Kompletni tekstove sa slikama i prilozima potražite u magazinu
"PLANETA" - štampano izdanje ili u ON LINE prodaji Elektronskog izdanja
"Novinarnica"
|

