TEMA BROJA

Borka Marinković

Piramide - tajne i otkrića

Građevine i drevni matematičari

Na mestu gde je bio stari sumerski grad Nipur, u blizini hrama u obliku stepeničaste piramide (zigurat) nađeno je oko 50.000 glinenih pločica od kojih mnoge ukazuju da su Vavilonci i stari Egipćani imali solidno znanje matematike. Najčešće se pominje Ahmes (1600. godine pne), tvorac najstarijeg matematičkog dela, pisanog hijeroglifima na papirusu (Rhindov papirus koji se čuva u Londonu).

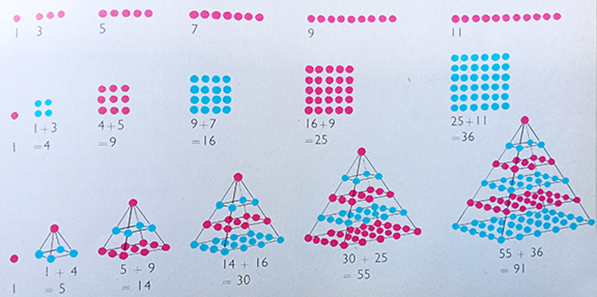
Vavilonci su još dve hiljade godina pne razumeli povezanost algebre i geometrije.  Određeni nizovi brojeva predstavljali su algebarski prikaz geometrijskih figura: trougaoni brojevi predstavljani su nizom 1, 3, 6, 10, 15.., tetraedarski (tetraedar je pravilan poliedar sastavljen od 4 jednakostranična trougla) brojevi predstavljani su nizom 1, 4, 10, 20, 35.., kvadratni brojevi 1, 4, 9,16, 25.., piramidalni brojevi 1, 5,14, 30, 55...

Piramidalni brojevi

1=(1*2*3)/(1*2*3), 5=(2*3*5)/(1*2*3), 14=(3*4*7)/(1*2*3),
30=(4*5*9)/(1*2*3), 55=(5*6*11)/(1*2*3).

Na crtežu je prikazan način formiranja piramidalnog niza.
Poznavanje piramidalnih brojeva omogućilo je kasnije lako određivanje broja  kugli municije pri skladištenju municije u obliku piramide.
Egipćani su znali formulu za izračunavanje zapremine piramide. Na Moskovskom papirusu (oko 1850. godine pne) koji sadrži matematičke tekstove starog Egipta, zapisana je i formula za izračunavanje zapremine zarubljene kvadratne piramide (piramida kojoj je odsečen vrh na određenoj visini tako da, umesto jedne osnove, ima dve):

V=1/3h(a2 +ab+b2), pri čemu su a i b stranice donje i gornje osnove (kvadrati), a h je visina piramide.

Matematika je imala ključnu ulogu u arhitekturi i prilikom astronomskih izračunavanja. Da bi se fiksirao meridijan i prema njemu izgradila piramida čije su strane bile precizno usmerene ka stranama sveta, a čiji je najbolji primer Velika piramida u Gizi, bilo je potrebno prepoloviti ugao kojeg čine položaji izlaska i zalaska Sunca na dan ravnodnevnice. Pretpostavlja se da su drevni graditelji, za konstrukcije, koristili konopac i štapove kao improvizovani šestar za crtanje na pesku. Iako se radilo o vrlo primitivnim alatima, greška pri ovim konstrukcijama i izračunavanjima stranica piramida manja je od 1%. To pokazuje da su Egipćani znali za osnove Pitagorine teoreme i povezanost veličina stranica (a 2+b2=c2). Praveći čvorove na kanapu na razmacima 3-4-5 i savijajući ga na mestima čvorova, dobijali su pravougli trougao. Osim ove Pitagorejske trojke, poznavali su još 15 trojki brojeva koji mogu biti dužine stranica pravouglog  trougla: (5,12,13), (7,24,25), (8,15,17), (9,40,41) itd.
Takođe, poznavali su neke osobine kruga. Tangentu u tački dodira kružnice normalnu na dodirni poluprečnik koristili su za astronomska izračunavanja. Ugao nad prečnikom kruga je uvek prav ugao, što je važna osobina za konstrukciju pravog ugla. Za razliku od njihovih savremenika, Egipćani su došli do najbliže vrednost broja π (16/9)2= 3,16.

Geometrijska definicija piramide

Piramida je geometrijsko telo (poliedar) kojeg čine osnova i bočne strane (omotač). Osnova može biti bilo koji mnogougao. U zavisnosti od broja njegovih stranica je broj bočnih strana (trouglova) pa se piramide nazivaju: trostrana, četvorostrana, petostrana itd.
Sve bočne ivice seku se u jednoj tački koja se naziva vrh piramide. Visina piramide je duž koja polazi iz vrha i normalna je na osnovu piramide. Apotema je visina bočne strane piramide (trougla).
Piramida može biti prava ili kosa. Ukoliko je osnova prave piramide pravilan mnogougao, i piramida je pravilna i tada su bočne strane jednakokraki (posebno jednakostranični) trouglovi. Tetraedar je pravilna jednakoivična trostrana piramida koju čine 4 podudarna jednakostranična trougla.

Borka Marinković

Kompletni tekstove sa slikama i prilozima potražite u magazinu
"PLANETA" - štampano izdanje ili u ON LINE prodaji Elektronskog izdanja
"Novinarnica"