MATEMATIKA
Borka Marinković
Srednjevekovna znanja
Zadaci za gimnastiku uma
Da li je srednji vek u Evropi bio „mračanˮ i za matematiku? Dobri poznavaoci istorije matematike teško mogu da navedu nekog velikog matematičara ili značajne matematičke rezultate iz tog vremena. Mnogima nepoznati Alkuin od Jorka baca novo svetlo na srednjevekovnu matematiku i njeno obrazovanje. Po dokazima, istina nepotpunim, Alkuin je autor zbirke „Zadaci za gimnastiku umaˮ. Ta zbirka se pominje u zanimljivoj matematičkoj prepisci dvojice kaluđera iz Kelna i Liježa iz 1025. godine pod nazivom „Albinusˮ, što je latinsko ime za Alkuina.

Da li je srednji vek u Evropi bio „mračanˮ i za matematiku? Dobri poznavaoci istorije matematike teško mogu da navedu nekog velikog matematičara ili značajne matematičke rezultate iz tog vremena. Mnogima nepoznati Alkuin od Jorka baca novo svetlo na srednjevekovnu matematiku i njeno obrazovanje. Po dokazima, istina nepotpunim, Alkuin je autor zbirke „Zadaci za gimnastiku umaˮ. Ta zbirka se pominje u zanimljivoj matematičkoj prepisci dvojice kaluđera iz Kelna i Liježa iz 1025. godine pod nazivom „Albinusˮ, što je latinsko ime za Alkuina.
„Zadatak o čoveku, kozi i vukuˮ
Svima nam je, još iz detinjstva, poznata mozgalica kako da čovek, vuk, koza i kupus pređu reku, pri čemu treba voditi računa da se vuk i koza, koza i kupus ne smeju istovremeno naći na istoj obali. Alkuin preuzima ulogu skeledžije i rešava problem u koracima: “Prvo bih prvo preveo kozu. U drugom koraku bi vozio vuka, ali bih vratio kozu i ostavio je na obali. U sledećoj vožnji prevezao bih kupus. U poslednjoj vožnji bih prevezao kozu. Tako bih izbegao bi sve opasne situacije.”
„Zadatak o nekom ocu i njegova tri sinaˮ
Neki otac je umro ostavivši u nasleđe trojici sinova 30 staklenih balona - od kojih su 10 bili puni ulja, 10 su bili ispunjeni do pola, a preostalih 10 su bili prazni. Zadatak: neka podeli onaj ko može ulje i balone, ali tako da svakom od tri sina pripadne jednako balona i ulja.
Alkuinovo rešenje: izračunaj 3x10 = 30. Svaki sin dobija 10 balona kao svoj deo. Podeli na tri dela, tj. daj prvom sinu 10 polupunih, drugom i trećem po pet punih i pet praznih. Tako će delovi na koje su podeljeni baloni i ulje biti jednaki.

Alkuin od Jorka
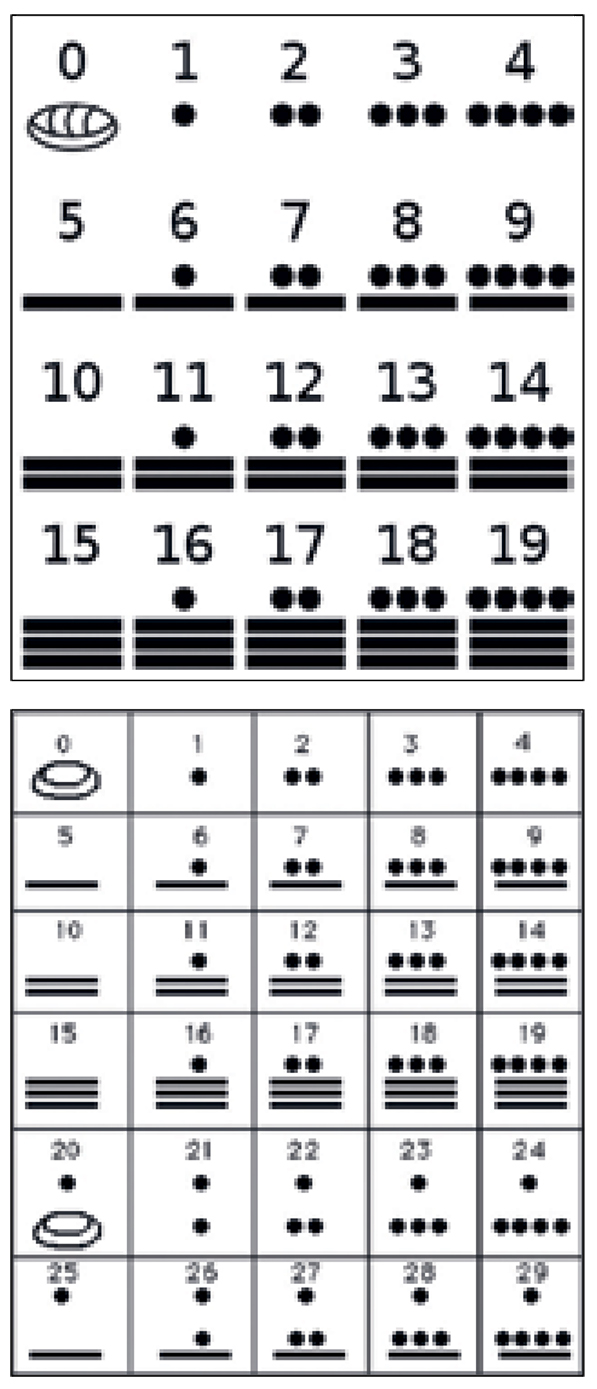
Tablica brojnog sistema sa
osnovom 20 i proširena tablica
sa vrednostima do 29 |
„Zadatak u kojem dečak pozdravlja svog ocaˮ
Neki dečak se obratio svom ocu rekavši: „Oče moj, da si mi zdravo!ˮ Otac je odgovorio: „Zdrav bio, sine moj! Da doživiš tri puta dvostruki broj tvojih godina. Tada ćeš, ako dodaš jednu moju godinu, imati 100 godina.ˮ Neka kaže onaj ko može koliko je godina imao dečak u tom trenutku...
Alkuinovo rešenje: dečak je imao 16 godina i 6 meseci. Kada se taj broj udvostruči, dobiju se 33 godine koje, utrostručene, daju 99. Na taj broj se doda jedna očeva godina, što je ukupno 100 ( jednačina 2x3xX+1=100).
Matematika Maja sa osnovom 20
Istorija civilizacije Maja, kao i istorija ostalih srednjeameričkih civilizacija, može se podeliti na tri razdoblja: preklasični period - od 2500. godine pne do 3. veka ne, klasični period - od 3. do 9. veka, i postklasični period - od 9. do 16. veka.
Do danas su sačuvane samo četiri knjige Maja, takozvani kodeksi (Grolier Codex, Dresden Codex, Troano Codex i Paris Codex), svi napisani u postklasičnom periodu. Pismo Maja je tek tokom 20. veka uspešno dešifrovano zajedničkim naporom brojnih naučnika, i danas se smatra jedinim njihovim dešifrovanim pismom.
Takođe, radarski snimci visoke rezolucije i satelitski snimci zajedno sa dešifrovanim knjigama, promenili su poimanje Majanske civilizacije. A zajednička kultura, kalendar i mitologija bili su okosnica civilizacije. Astronomija je igrala važnu ulogu u religiji, a astronomski i kalendarski proračuni ne mogu se zamisliti bez matematičkog znanja i korišćenja njenih alata.
Maje su izgradili jedinstven brojni sistem koji je bio daleko najnapredniji od bilo kog drugog u to vreme. Reč je o brojnom sistemu sa osnovom 20. Iako se danas ta osnova čini neupotrebljivom, posredi je prirodna osnova koja proističe od ukupnog broja prstiju na rukama i nogama, pomoću kojih su Maje vršili razna izračunavanja. U prilog tome ide značaj mesta broja 5. Sistem je dobio ime: vigezimalni brojni sistem. Iako se radi o glomaznoj osnovi (heksadecimalni sistem, koji se koristi u računarstvu, ima osnovu 16 i za zapis brojeva u ovom sistemu je potrebno, osim naših 10 cifara, još 5 simbola koje čine slova: A, B, C, D i E).
Maje su koristile samo 3 simbola: nula je predstavljena oblikom školjke, jedinica je predstavljena tačkom (kamenčićem) a pet - crtom (štapom). Brojevi su zapisivani u nekoj vrsti pozicionog sistema. Cifre nekog broja su zapisivani odozgo ka dole, tako da prva cifra ima najveću numeričku vrednost.
Sabiranje i oduzimanje pojedinačnih cifara (brojeva manjih od 20) veoma je jednostavno u brojnom sistemu Maja. Na primer, prilikom sabiranja, dovoljno je crtice i tačkice dve cifre spojiti u jednu novu cifru. Ista pravila su primenjivana u sabiranju i oduzimanju većih brojeva od 20. U tako koncipiranom pozicionom brojnom sistemu, prva cifra odozdo ima samo „cifarskuˮ vrednost, cifra iznad „poseduje težinuˮ 20, itd.
Iako bi i množenje i deljenje brojeva moglo lako da se vrši postupcima nalik na one za decimalni sistem, do sada nisu pronađeni nikakvi dokazi da su Maje vršile množenje i deljenje. Takođe, ne postoje dokazi da su Maje koristile negativne brojeve, razlomke ili nešto nalik na decimalnu tačku.
Cifre koje su koristili bile su podložne menjanju isto koliko i pismo Maja. Tako se u nekim tekstovima mogu videti promena orijentacije cifara, različito stilizovanje (posebno cifre 0), kao i spajanje s logogramima. Takođe, Maje su imale alternativne zapise za brojeve do 20, u obliku glava bogova. Tako je s glavom boga vetra bio predstavljen broj 3, s glavom boga Meseca broj 4, s glavom boga smrti broj 10 i tako dalje... Ovakvi zapisi oslikavaju numerološka verovanja Maja.
Merenje vremena
Maje su male dva kalendara. Jedan je bio ritualni, sastavljen od 260 dana. Sadržavao je 13 meseci od po 20 dana , a imena meseca su davana po bogovima. Drugi je brojao 365 dana i sastojao se od 18 meseci, a nazivi su bili prilagođeni poljoprivrednim ili verskim događajima (18x20=360). Postojao je i jedan „kratki mesecˮ od samo 5 dana, koji je smatran za nesrećni period. Dani u oba kalendara su bili numerisani od 0 do 19.
Astronomska merenja Maje su vršili gledajući kroz prav ugao dobijen ukrštanjem štapova. Za savremene alate i mogućnosti merenja, nezamisliva je preciznost koju su postizali tako skromnim instrumentima. Oni su izračunali dužinu godine 365, 242 dana (savremena vrednost je 365, 242198 dana). Izvanredna dostignuća su postigli u računanju dužine lunarnog meseca. U Kopanu (na granici Hondurasa i Gvatemale), Maje su otkrile da je 149 lunarnih meseci trajalo 4400 dana (dužina dana 4400/149 =29.5302). Slično, u Palenkueu su izračunali da je 81 lunarni mesec trajao 2392 dana (2392/81=29.5308). Savremena vrednost je 29, 53059.

Neverovatna geometrija
U četiri sačuvane knjige iz perioda Maja nema podataka koji bi precizno ukazali na geometrijska znanja koje su Maje posedovale. Međutim, analizom hramova, kuća, opservatorija, puteva i gradova koji su sačuvani do današnjih dana u džunglama Srednje Amerike, postaje jasno da su Maje morale posedovati osnovna znanja iz geometrije. Maje su sa neverovatnom preciznošću konstruisale prave uglove i paralelne linije prilikom gradnje pomenutih objekata.
Takođe, u slikama (u kodeksima, na grnčariji i na zidovima) koje su sačuvane do danas, moguće je primetiti upotrebu lenjira i šestara.
Borka Marinković
Kompletni tekstove sa slikama i prilozima potražite u magazinu
"PLANETA" - štampano izdanje ili u ON LINE prodaji Elektronskog izdanja
"Novinarnica"
|

